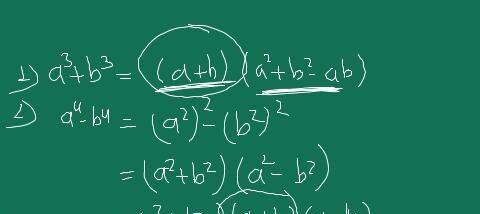Mathematics, often hailed as the universal language of the cosmos, boasts a wealth of formulas, equations, and concepts. Among these mathematical treasures, the A3+B3 formula, also known as the sum of cubes, stands out as a particularly captivating and enigmatic algebraic expression. In this extensive exploration, we embark on a journey to uncover the depths of this mathematical marvel, tracing its historical roots, unraveling its core algebraic identity, examining its wide array of applications, and appreciating its enduring significance in the realm of mathematics.
Understanding the A3+B3 Formula
The A3+B3 formula, seemingly simplistic yet profoundly captivating, symbolizes the sum of two cubes, each represented by the variables A and B. At its core, this algebraic gem can be distilled to its most fundamental form: A3+B3. This expression encapsulates the third power of two distinct real numbers, A and B, whose addition yields a result that reverberates throughout the mathematical cosmos.
Historical Context
The origins of the A3+B3 formula are deeply embedded in the annals of mathematical history, with luminaries such as Diophantus and Fermat laying the groundwork for its exploration. However, it was the brilliant Swiss mathematician Leonhard Euler who made significant strides in the 18th century, shedding light on the formula and paving the way for a comprehensive understanding of its applications and implications.
Algebraic Insights
To unravel the secrets of the A3+B3 formula, we must dissect its components: A and B represent tangible, real numbers, each with its unique value. A3 denotes the cube of A, while B3 signifies the cube of B. The act of adding A3 and B3 results in the sum of these cubes, serving as a gateway to a profound mathematical world where the properties of cubes intertwine, offering insights into their interactions and sparking curiosity.
Practical Applications
The versatility of the A3+B3 formula extends across diverse mathematical landscapes, serving as a valuable tool in algebraic manipulations, number theory, and cryptography. In some cases, it forms the cornerstone for solving intricate equations, leaving an indelible mark on the mathematical universe.
Geometry and Beyond
Even in the realm of geometry, characterized by shapes, sizes, and spatial dimensions, the allure of the A3+B3 formula remains palpable. It finds a natural home in solving volume-related problems, as the cube of a number often represents three-dimensional space, enriching geometric calculations and the exploration of various shapes.
Variations and Expansions
Driven by curiosity, mathematicians continually explore variations and expansions of the A3+B3 formula, unearthing new dimensions of its applications and paving the way for groundbreaking discoveries. These endeavors exemplify the ever-evolving nature of mathematics and its capacity for innovation.
Simplification and Real-World Relevance
While the A3+B3 formula may initially appear daunting, various methods have been devised to simplify it, making it more accessible for solving equations and addressing real-life problems in fields ranging from engineering to physics. Its abstract nature finds tangible relevance in practical applications, bridging the gap between theory and reality.
Conclusion
In conclusion, the A3+B3 formula, with its simplicity and profound implications, serves as a testament to the timeless allure of mathematics. From its humble historical origins to its modern-day applications, this algebraic gem continues to captivate mathematicians and enthusiasts alike, inspiring curiosity, innovation, and a deeper appreciation for the boundless possibilities of mathematical exploration.