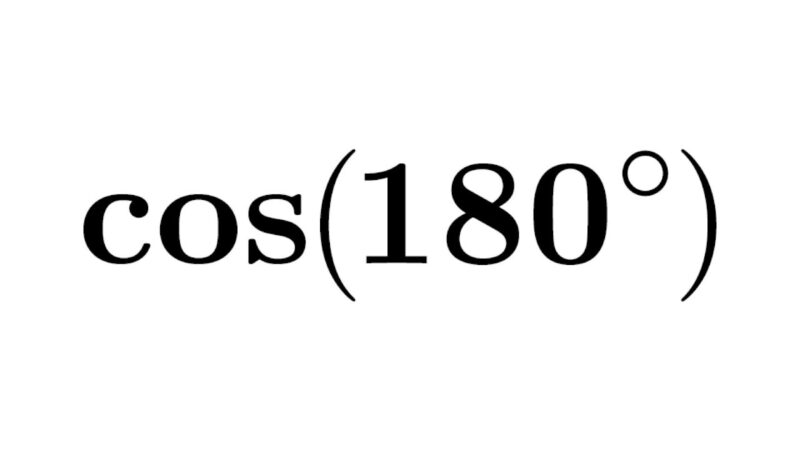The cosine function, often denoted as cos(θ), stands as one of the six fundamental trigonometric functions utilized to establish connections between the angles within a right triangle and the ratios of its sides. Within a right-angled triangle, the cosine of an angle represents the ratio of the adjacent side’s length to that of the hypotenuse. This function, periodic in nature, oscillates between -1 and 1 as the angle varies, serving as a cornerstone in various disciplines including mathematics, physics, engineering, and beyond.
Understanding Cos 180:
Cos 180 entails evaluating the cosine function at an angle of 180 degrees. The value of cos(180°) is -1, indicating a negative length for the adjacent side relative to the hypotenuse in a right triangle with a 180-degree angle. A unique aspect of Cos 180 lies in its depiction of the horizontal component of a vector with a 180-degree direction in the Cartesian plane, which can be a complex concept. Mastery of Cos 180 proves vital within trigonometry, forming a solid foundation for further exploration within the subject.
Applications of Cos 180 in Trigonometry:
The concept of Cos 180 finds widespread applications across various trigonometric problems and real-world scenarios. One significant application lies in understanding reflections and rotations. When an object undergoes a 180-degree rotation, the cosine function aids in determining the resulting positions of its points. Moreover, Cos 180 plays a crucial role in the analysis of periodic functions such as waveforms and oscillations, particularly in fields like signal processing and music theory.
Trigonometric Ratios and Cos 180:
Trigonometric ratios refer to the relationships between the sides of a right triangle and its angles. Cos 180 represents one of these ratios, indicating the relationship between the adjacent side and the hypotenuse in a right triangle with a 180-degree angle. These ratios, including Cos 180, are extensively employed in problem-solving across various mathematical branches like geometry and calculus.
The Unit Circle and Cos 180:
The unit circle serves as a fundamental tool for correlating angles with coordinates in the Cartesian plane. At 180 degrees, the cosine function reaches its lowest point, represented as (-1, 0) on the unit circle. This point holds significance in understanding the periodic nature of the cosine function. Beyond aiding in the visualization of trigonometric functions, the unit circle finds applications in physics, engineering, and computer graphics.
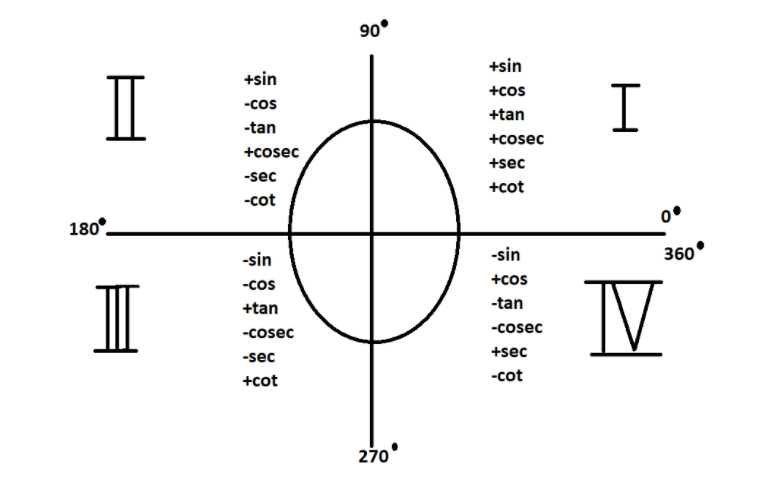
Graphical Representation of Cos 180:
Graphing the cosine function for different angles produces a cosine curve, a periodic wave. At 180 degrees, the cosine curve reaches its minimum value of -1. This graphical representation allows for visualizing the behavior of Cos 180 across various angles, with applications spanning sound waves, vibrations, and harmonic motion.
Evaluating Cos 180 in Degrees and Radians:
Angles can be measured in degrees or radians, necessitating an understanding of their conversion. When evaluating Cos 180, its value remains consistent regardless of whether the angle is expressed in degrees or radians, remaining -1. This conversion proves essential when dealing with trigonometric functions in calculus and advanced mathematical applications.
Cos 180 in Real-life Scenarios:
Cos 180 finds practical utility in numerous real-life scenarios. For example, it aids in analyzing sound waves, where a 180-degree phase shift can lead to constructive or destructive interference. Additionally, understanding the behavior of Cos 180 proves crucial in navigation, astronomy, and mechanical engineering, where it facilitates the determination of positions, distances, and the movement of rotating components.
Cos 180 in Physics and Engineering:
In physics and engineering, Cos 180 serves as a fundamental tool for solving a diverse array of problems. It finds application in analyzing oscillatory motion, calculating work done against gravitational forces, and designing motion systems, robotics, and electrical circuits.
Cos 180 in Mathematics and Calculus:
Within mathematics, the cosine function plays a pivotal role in various concepts and calculations. In calculus, it aids in integration and differentiation, facilitating the solution of differential equations and the analysis of functions, especially those involving trigonometric functions.
Other Trigonometric Functions Related to Cos 180:
Cos 180 shares relationships with other trigonometric functions such as sine and tangent, which can be expressed using identities to simplify trigonometric equations, offering shortcuts in problem-solving.
Importance of Understanding Cos 180:
Comprehending Cos 180 extends beyond an academic exercise, bearing profound implications in scientific and engineering disciplines. It serves as the bedrock for delving into advanced trigonometric concepts and their practical applications, essential in fields like physics, engineering, surveying, and architecture.
Common Mistakes and Misconceptions about Cos 180:
Students often encounter common misconceptions, such as conflating the values of Cos 180 with Cos 0 or assuming Cos 180 is positive akin to cosine values for acute angles. Rectifying these misconceptions fosters a deeper understanding of trigonometry and enhances problem-solving prowess.
Tips for Solving Problems Involving Cos 180:
Here are some useful strategies for solving problems involving Cos 180 and other trigonometric functions, essential for excelling in trigonometry and related fields:
- Begin by identifying the angle provided in the problem and understanding its context.
- Determine whether the angle is given in degrees or radians, and convert it if necessary to ensure consistency.
- Utilize the definition of the cosine function to establish the ratio of the adjacent side to the hypotenuse in the relevant triangle.
- Apply any pertinent trigonometric identities or formulas to simplify the problem and streamline your calculations.
- Finally, thoroughly evaluate the final result to ensure its coherence and relevance within the given context.
Conclusion:
Cos 180, with a value of -1, holds significant sway in trigonometry, mathematics, and various scientific and engineering domains. Its applications extend to real-world scenarios, aiding in the analysis of waveforms, rotations, and oscillations. A comprehensive grasp of Cos 180 empowers individuals to tackle complex problems and gain valuable insights into angle behavior and periodic functions, proving indispensable across diverse fields of application.