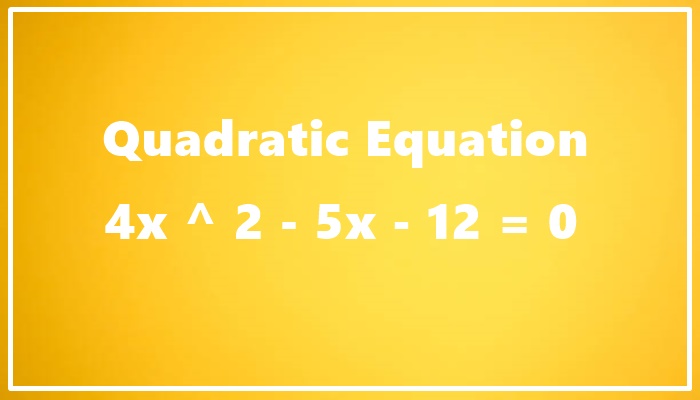Quadratic equations serve as foundational elements in algebra, manifesting across various mathematical and scientific domains. This comprehensive exploration focuses on the quadratic equation 4x^2 – 5x – 12 = 0, delving into its solutions and offering insights applicable to similar equations.
Understanding the Quadratic Equation 4x^2 – 5x – 12 = 0
Quadratic equations, being polynomial equations of the second degree, conform to the standardized form: ax^2 + bx + c = 0. Here, ‘a,’ ‘b,’ and ‘c’ represent constants, while ‘x’ denotes the variable. The equation in focus, 4x^2 – 5x – 12 = 0, indeed falls under this category.
These equations hold significance in mathematics and science due to their ability to model real-world phenomena, ranging from projectile motion to population growth. Thus, mastering methods to solve them is paramount across various disciplines.
Significance of Quadratic Equations 4x^2 – 5x – 12 = 0
Quadratic equations find application in diverse fields, making them indispensable in both mathematical realms and practical applications. Their importance is evident in:
Physics: Quadratic equations describe object motion influenced by gravity. For example, when determining the trajectory of a launched projectile, quadratic equations come into play.
Engineering: Engineers utilize quadratic equations in structural design, electrical circuit analysis, and mechanical behavior prediction, aiding in optimizing designs and ensuring system safety and functionality.
Economics: In economics, quadratic equations model revenue, cost, and profit functions, aiding businesses in profit maximization and cost minimization strategies.
Biology: Biologists employ quadratic equations to study population dynamics, organism growth, and disease spread, enabling predictions and management strategies for biological systems.
Solving 4x^2 – 5x – 12 = 0
Factoring Method:
One common approach to solving quadratic equations is factoring, which involves rewriting the equation to facilitate finding ‘x’ values that satisfy it. To factor 4x^2 – 5x – 12 = 0, we seek two numbers whose product equals the product of ‘a’ and ‘c’ (4 * -12 = -48) and whose sum equals ‘b’ (-5). These numbers are -8 and 6.
We rewrite the equation as (4x^2 – 8x) + (3x – 12) = 0.
Grouping and Factoring:
Grouping terms with common factors, we factor them separately: 4x(x – 2) + 3(x – 4) = 0.
Both terms share (x – 2) as a common factor: (x – 2)(4x + 3) = 0.
Solving for ‘x’:
Setting each factor to zero, we solve:
x – 2 = 0 → x = 2
4x + 3 = 0 → 4x = -3 → x = -3/4
Conclusion
In conclusion, proficiency in solving quadratic equations like 4x^2 – 5x – 12 = 0 is invaluable, given their broad applicability across mathematics, science, and practical scenarios. We’ve explored the factoring method as a potent tool for solving such equations, though other methods like the quadratic formula and completing the square also prove effective.