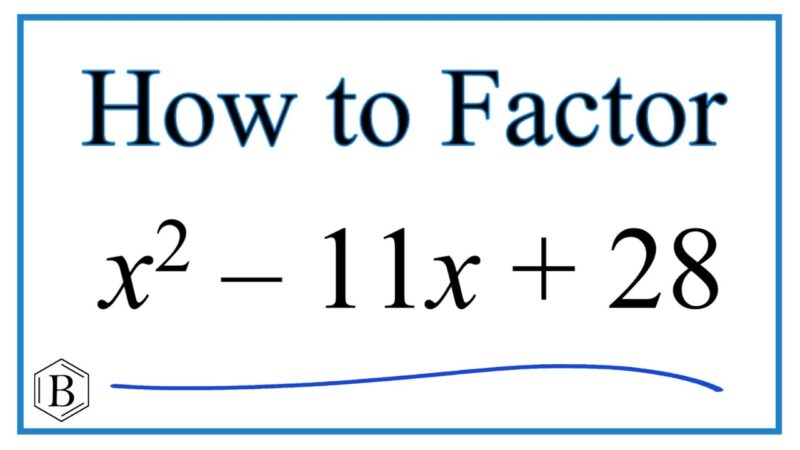Welcome to an exploration of quadratic equations, a fundamental aspect of algebra and mathematics. This article aims to delve into the intricacies of quadratic equations, with a specific focus on the equation x²-11x+28=0. Throughout this discourse, we will elucidate the general concept of quadratic equations, examine different methods to solve them, and delve into a detailed case study to illustrate their practical applications.
Understanding Quadratic Equations x²-11x+28=0
Before delving deeper, let’s establish a foundational understanding of quadratic equations. A quadratic equation is a second-degree polynomial equation, characterized by the presence of a squared variable. The canonical form of a quadratic equation is represented as:
ax^2 + bx + c = 0
Here, ‘a,’ ‘b,’ and ‘c’ denote coefficients, while ‘x’ represents the variable. The equation x²-11x+28=0 perfectly adheres to this standard form.
General Form of a Quadratic Equation
A grasp of the general form of quadratic equations is crucial as it forms the basis for understanding these equations. By recognizing this structure, we can easily discern the coefficients ‘a,’ ‘b,’ and ‘c.’ For our specific equation, ‘a’ equals 1, ‘b’ equals -11, and ‘c’ equals 28.
Solving Quadratic Equation x²-11x+28=0
Quadratic equations present mathematical challenges that can be addressed through various methods. Let’s explore two prominent techniques:
Factoring
Factoring is a method used for solving quadratic equations that can be easily decomposed. However, for equations as intricate as x²-11x+28=0, factoring might not be the most straightforward approach.
Quadratic Formula
The quadratic formula emerges as a versatile and universally applicable method for solving quadratic equations. This formula, frequently employed, is:
x = (-b ± √(b^2 – 4ac)) / 2a
Using this formula, we derive the roots of the equation, representing the values of ‘x’ that satisfy the equation.
x^2-11x+28=0: A Case Study
Now, let’s focus on the specific equation x^2-11x+28=0. We will conduct a step-by-step analysis using the quadratic formula.
Step 1: Identifying the Coefficients
To begin, we identify the coefficients. In the given equation, ‘a’ is 1, ‘b’ is -11, and ‘c’ is 28.
Step 2: Applying the Quadratic Formula
With the coefficients determined, we apply the quadratic formula, resulting in:
x = (-(-11) ± √((-11)^2 – 4 * 1 * 28)) / (2 * 1)
Simplifying the equation, we obtain:
x = (11 ± √(121 – 112)) / 2
x = (11 ± √9) / 2
Step 3: Finding the Roots
Upon simplification, we discover two potential solutions:
x = (11 + 3) / 2 = 7
x = (11 – 3) / 2 = 4
Thus, the roots of the equation x^2-11x+28=0 are x = 7 and x = 4.
Graphical Representation of Quadratic Equations
In the realm of quadratic equations, graphical representations often manifest as parabolas. This U-shaped curve offers valuable insights into the behavior of these equations, with the vertex serving as a focal point, indicating either the minimum or maximum of the parabola.
Applications of Quadratic Equations
The practical utility of quadratic equations extends beyond theory, finding applications in diverse fields such as physics, engineering, and economics. In real-world contexts, quadratic equations serve as potent tools for modeling and resolving problems with precision.
Conclusion
In summary, our exploration of quadratic equations has been both engaging and enlightening. This article has elucidated the fundamental concepts underlying quadratic equations, delineated the methodology for solving them using the quadratic formula, and demonstrated their practical relevance through a specific case study, namely x^2-11x+28=0. Additionally, we’ve examined the graphical representation of quadratic equations through parabolic graphs and underscored their significance in various real-world applications.